Homography : 2D-2D 평면 변환

 

비전에서 가장 중요한 변환이

Homography 2D-2D 변환,

카메라 행렬 구하기 : 3D-2D 변환

스테레오 변환 행렬 E : 2D Point - 2D line 변환이다.

 

1. Homography 수식 유도

 

여기서 첫번째 Homography를 정리해보자.

먼저 이 H 변환은 2D에서의 변환이다. 즉 하나의 평면을 유지하는 가정이 중요하다.

여기서 x1과 x2가 homogenous 좌표계로 나타나 있다고 하면,

X1 = [xi yi zi] - homogenous 좌표계

X1 = [xi/zi yi/zi] - inhomogenous 또는 heterogenous 좌표계

로 나타낼 수 있다.

위 그림과 같이 2D-2D 변환은 여러가지가 존재하는데 PP3 평명을 2개의 카메라로

투영(Projective)하여 변환하였을 때 이 변환이 Homography이다.

pi, pi' 의 대응점이 주어졌을 때 변환 H를 찾아보자.

scale 을 모르므로 영상에서 p점을 homogenous 좌표계 P로 변경한다.

H를 곱해서 P를 P'으로 변환한다.

P'을 다시 heterogenous 좌표계로 변환한다. (w'으로 나누어서 1을 떼면 됨)

 

두점을 먼저 homogenous 좌표로 나타낸 식을 행렬로 나타내보자.

단여기서 주의할 점은 scale a 가 들어가야한다는 점이다. 다른 변환과 비교해보자.

순서를 정리하여 우리가 알고싶은 H를 벡터로 몰아놓으면,

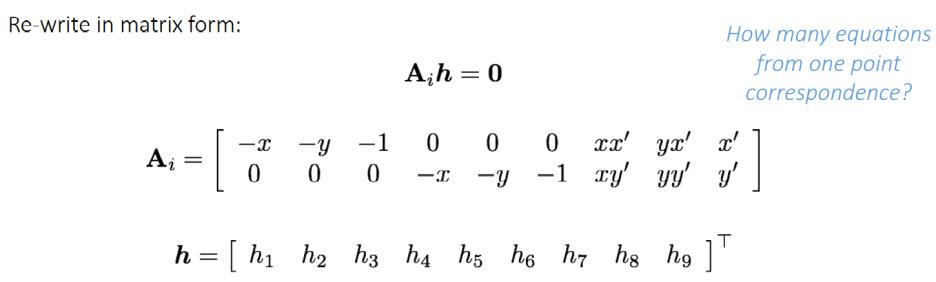
대응점을 여러개 있다고 한다면,

대표사진 삭제

사진 설명을 입력하세요.

수식은 유도가 되었으므로 어떻게 풀어야 되는지 생각해보자.

위의 식은 A의 영공간에서 h가 존재한다는 의미이다. 그리고 non-trivial 해가 있다는 의미이다.

가장 일반적인 투영geometry 에서의 형태는 x = Ay의 꼴이다. 여기서 x, y는 known이다.

단, 여기서 equality 는 단지 up-to-scale 에만 만족한다.

이것은 다음 식을 만족한다는 의미이며 ordinary least square 를 쓸 수 없는 이유이다.

그래서 LDT를 보통 이용한다.

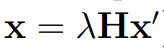
2. LDT를 이용하여 H 구하기

 

여기서 Linear Direct 방법을 쓰자.

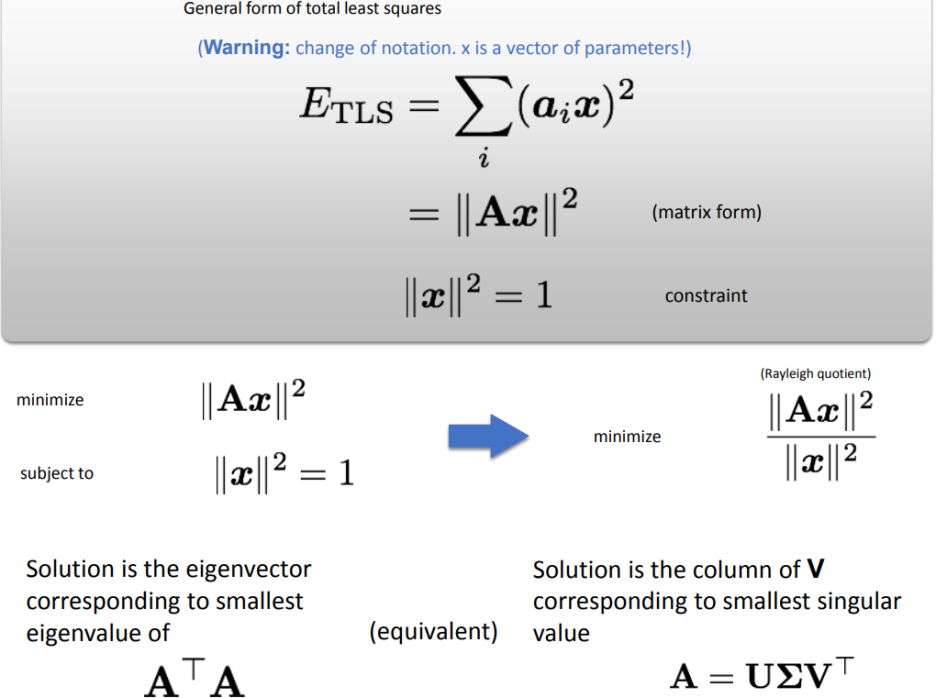
위의 식이 선형 방정식이므로, SVD 등으로 분해하여 h를 찾아내는 것이다.

SVD로 분리하면

U는 othogonal 행렬로 left singular vector라고 하고,

Σ는 대각행렬로 각 요소는 eigen value를 나타내고, 크기의 순으로 정렬이 된다.

V는 right singular vector로 이 마지막 열벡터를 이용하여 순서대로 행렬로 만드면 그것이 우리가 원하는 H 행렬이 된다.

 

만약 9x9 행렬의 경우

σ9 = 0이면 exactly-determined 이며, homography 가 존재하고 모든 점은 exactly 하게 fit하다.

σ9 > 0이면 voer-determined 이며, homography 가 존재하나 모든 점이 exactly 하게 fit하지 않다. (=least square 관점에서만 fit하다)

적어도 4개의 대응점을 가질 것이지만 그렇지 못할 경우 시스템은 under-determinded 이다.

 

여기서 U의 열은 AA' 의 eigenvalue이며, V의 열은 A'A의 eigenvalue 이다.

 

우리가 관심을 갖는 Ax=0 식으로 다시 돌아가자.

Ah가 0에 가깝도록 구성하는 h를 찾아보자. 즉 Ah-0 의 square-sum 오차가 최소가 되도록 cost function을 정의하면,

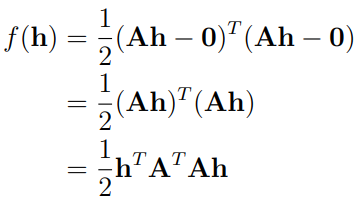
제곱이 최소가 되기 위한 h를 찾기위해 위 식을 h로 미분하면,

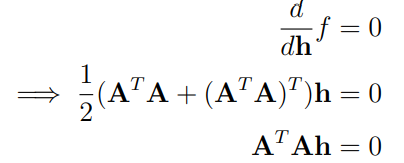
이는 h의 값이 zero eigen value(잡음이 0에 가까운)에 대응하는 eigen vector와 같다는 의미이다.

그리므로 우리는 A'A의 가장 작은 eigenvalue를 선택한다.

3x3 행렬일 경우 σ9가 되고 이에 대응하는 V의 eigen vector가 Ah=0의 해가 될 것이다.